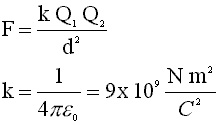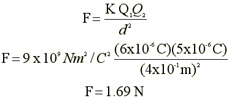ELECTRIC FIELDS &
FORCES
 Forces of attraction and repulsion among non-metallic
substances were reported in early Greek times. Artisans found
that when they cut and polished amber (hardened tree sap) to make
jewelry, the amber attracted or repelled bits of paper, hair,
and other light-weight, non-metallic materials. One can imagine
that one of the eye-catching features of this phenomenon is the
idea of action-at-a-distance. Whereas in most cases if a person
wishes to cause an object to move, he or she must physically touch
the object to pull or push it. However, with the phenomenon we
now call electrostatic attraction/repulsion, objects interact
with each other with no physical contact.
Forces of attraction and repulsion among non-metallic
substances were reported in early Greek times. Artisans found
that when they cut and polished amber (hardened tree sap) to make
jewelry, the amber attracted or repelled bits of paper, hair,
and other light-weight, non-metallic materials. One can imagine
that one of the eye-catching features of this phenomenon is the
idea of action-at-a-distance. Whereas in most cases if a person
wishes to cause an object to move, he or she must physically touch
the object to pull or push it. However, with the phenomenon we
now call electrostatic attraction/repulsion, objects interact
with each other with no physical contact.
 |
The study of electrostatics
became quite popular among natural philosophers in the seventeenth and
eighteenth centuries. Prominent among these was Benjamin Franklin who,
when not working as a founding father or as an ambassador to France,
found time to do elementary research into the nature of electricity. He
had some successes, showing that lightning was in fact an electrostatic
phenomenon and inventing the lightning rod to protect buildings. And
like any other thinker who dares to speculate on what might be true, he
held some beliefs that were later shown to be less than correct. For
instance, he believed that electric charge was a single "fluid". An
object was positively charged if it had an excess of fluid, negatively
charged if it had a deficiency. (This scheme is not unlike our modern
view of heat where an object is hot if it contains lots of heat energy,
cold if it does not.)
For a look at Benjamin Franklin the
scientist, go to
http://www.fi.edu/franklin/
|
The modern view of charge can
be summarized by four simple statements.
1. There are two kinds of charge.
2. Like charges repel.
3. Unlike charges attract.
4. Charge is quantized.
The fourth statement, that charge
exists in discreet lumps, is a twentieth century notion that we
will revisit when we get to modern physics.
 |
The idea that charges repel and attract one
another was quantified by the French scientist Charles Coulomb who used
a sensitive torsion balance to measure the forces between charged
objects. He concluded that these forces were directly proportional to
the product of the charges and inversely proportional to the square of
the distance between them. The form of this relationship, later named
Coulomb's law, looks remarkably like Newton's law of universal
gravitation, a fact that has prompted scientists to look for connection
between the two rules ever since. |
Coulomb's Law
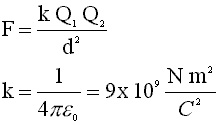 |
|
Unit of charge
The SI unit of charge is the Coulomb,
named after you-know-who, and represents a number of charges,
specifically
1C = 6.25 x 10^18 charges
Ten to the eighteenth power
seems like a big number and it is compared to most things that we
count. But let's put it in context with something like Avogadro's
number, about 10^23. Let's say we have a mole of copper (about 63 g)
and we wish to give this object a residual charge of one Coulomb of
positive charge. To do this, we must remove 10^18 electrons. A mole of
atoms could be divided into 10^18 piles of 10^5 atoms. We get a Coulomb
by removing 1 electron from each pile of 100,000.
|
Sample
Problem - Coulomb's
Law
| Let us consider two
charges Q1 = +6 x 10^-6 C and Q2 = 5 x 10^-6 C separated by a distance
of .4 m Determine the magnitude and direction of the force acting on
each charge |
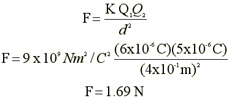 |
| Because both
charges have the same sign, the forces are repelling and F21 points left. The
is no easy way to generate a negative sign show this. The safest
strategy is to report that F21 = 1.69 N points left |
 |
Problem-solving
strategies
1. Solve force problems for the absolute value of F. Do not install +
and -.
2. If more than one charge acts on a given charge, apply Coulomb's law,
pairing the charge in question with each of the others, and add the
forces vectorially |
why grounding
http://www.eskimo.com/~billb/amateur/whygnd.txt
THE ELECTRIC FIELD
| |
|
| To explain the
action-at-a-distance, we develop the idea of the electric field, a
region of interaction around any charged object that starts at the
charge and radiates (outward for positive charges, inward for
negatives) in all directions to infinity. Thus any charge falling in
this space (which is to say every charge in the universe) is either
attracted to or repelled by the charge causing the field. If we bring a
test charge into a space where a field exists, the charge will feel a
force which could be large or small. Let's say that the force is large;
is the large magnitude due to the field being large or that the test
charge is large. To determine field strength, we define a quantity
called Electric Field intensity E |
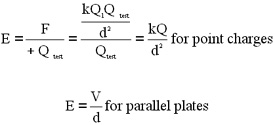 |
Let us draw an
analogy to gravitational fields. Pretend that we are visiting the
planet Glork and we attempt to move a small box. It turns
out the box is very heavy. Because w = mg still works
on Glork, we can conclude that either a) the box is very massive; or b)
the gravitational field on Glork is very strong
If we define gravitational field
initensity (GFI) to be force/ testmass we get the familiar g. Thus E is
to electric fields as g is to gravitional fields. It is important
to note that the gravitational field
is always ppresent everywhere around the mass that produced it.
So, too, is the electric field around a point charge..
|
 |
Consider three
point charges located at the corners of a square (side = a meters); the
fourth corner is vacant. Each charge creates a electric field
around itsef extending from the charge to infiinity in all directions
and necessarily has a piece of the action when it comes
|
See other supporting text at
http://theory.uwinnipeg.ca/physics/charge/node3.html#SECTION00120000000000000000
Try these applets
http://surendranath.tripod.com/FieldLines/FieldLines.html
http://www.cco.caltech.edu/~phys1/java/phys1/EField/EField.html
http://www.colorado.edu/physics/2000/applets/nforcefield.html
http://www.gel.ulaval.ca/~mbusque/elec/main_e.html
You will explore these ideas more thoroughly
by visiting the web sites listed below.
http://www.msms.doe.k12.ms.us/ap_physics/tutorials/chap6/chap6_2.html
http://www.glenbrook.k12.il.us/gbssci/phys/THender/quizzes/u8/q296.html
An exciting yet safe encounter with lightning
can be found at Boston's Museum of Science.
Visit the Theatre of Electricity at http://www.mos.org/sln/toe/toe.html
GO
TO ELECTROSTATIC PROBLEMS 1
SIDE BAR
Here are some useful sites for investigating practical applications
related to electric fields.
http://howthingswork.virginia.edu/electronic_air_cleaners.html
http://howthingswork.virginia.edu/xerographic_copiers.html
Exploratorium
http://www.exploratorium.edu/snacks/snacksbysubject.html
Return to E &
M home
 Forces of attraction and repulsion among non-metallic
substances were reported in early Greek times. Artisans found
that when they cut and polished amber (hardened tree sap) to make
jewelry, the amber attracted or repelled bits of paper, hair,
and other light-weight, non-metallic materials. One can imagine
that one of the eye-catching features of this phenomenon is the
idea of action-at-a-distance. Whereas in most cases if a person
wishes to cause an object to move, he or she must physically touch
the object to pull or push it. However, with the phenomenon we
now call electrostatic attraction/repulsion, objects interact
with each other with no physical contact.
Forces of attraction and repulsion among non-metallic
substances were reported in early Greek times. Artisans found
that when they cut and polished amber (hardened tree sap) to make
jewelry, the amber attracted or repelled bits of paper, hair,
and other light-weight, non-metallic materials. One can imagine
that one of the eye-catching features of this phenomenon is the
idea of action-at-a-distance. Whereas in most cases if a person
wishes to cause an object to move, he or she must physically touch
the object to pull or push it. However, with the phenomenon we
now call electrostatic attraction/repulsion, objects interact
with each other with no physical contact.