|
|
Potential Energy
We have seen in the previous section that like charges repel. Consider some charge +Q1 fixed at some point in space. If we bring a second charge, +Q2, from infinity and cause it to reside somewhere near the first charge, we will experience a force of repulsion along the way. That means that by overcoming that repulsive force over some distance we are doing work on the system. What happens to that work? We can find out if we release the second charge; it moves away, picking up speed and therefore acquiring kinetic energy along the way. Thus, the work that we did in bringing the two charges together can be stored temporarily as electric potential energy. It can be shown that for two charges Q1 and Q2 brought close together so that they are separated by some distance d, the electrical potential energy in the system is given by
|
|
Like all energy quantities, electrical potential
energy is a scalar. If both charges are alike, PEelec
is positive; some external agent (you)
must do work to cause the charges to assemble. If the charges
are oppositely signed, PEelec
is negative. We interpret this to mean
that the field will do the work to assemble the charges.
If we wish to assemble several charges in one neighborhood, the process of calculating PEelec is rather straightforward: 1) the first charge is placed without any work being done; 2) we then calculate the work done in bringing the second charge near the first; 3) now we calculate the work needed to bring the third charge near the first PLUS the work needed to bring the third charge near the second; 4) and so on. A few problems are included to test your understanding of what has been describes here.
These sites are links to an entire course
in E & M
http://theory.uwinnipeg.ca/physics/charge/node1.html
http://www.science.urich.edu/~rubin/pedagogy/132/132notes/EM.html
http://library.advanced.org/16600/intermediate/staticelectricity.shtml
http://www.phys.ufl.edu/~phy3054/extras/contents/Welcome.html
Electric potential
http://theory.uwinnipeg.ca/physics/charge/node1.html
 |
In the previous chapter we considered
force per unit charge as a measure of electric field intensity.
Yet another way to do this is to determine field strength electrical potential by measuring
work or energy per unit charge. Moving
charges from A to B may take a lot of energy because the field
is strong or because we are moving a lot of charge. Dividing
a change in system energy by the amount of charge should help.
For a point charge in space
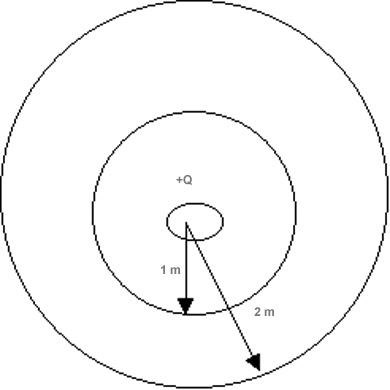
Let us calculate the potential at a point 1m away from a charge 1 x 10^-6 C (lower left box); then let's do it for 2 m. The answers suggest that it takes 9000 Joules/Coulomb to bring charges from infinity to the inner ring -- anywhere on the inner ring--(now called an equipotential line in 2D space}but only 4500 J/C to bring charge from infinity to the outer ring. |
|||
|
|
||||
A companion quantity to potential energy is electric potential. This quantity is very useful, but it is unfortunate that the names of the two terms are so similar as to be confusing to any careless reader. In the remarks immediately above, we sought to calculate the work necessary to bring a charge Q2 from infinity to some point P a distance d from Q1. We could have just as easily calculated the work necessary to to bring Q2 from infinity to some point P' a closer distance, d' , to Q1 (d'<d). If we take the difference in the amount of work thus calculated, we can determine the amount of work necessary to move Q2 from point P to point P'. This is useful because it eliminates the need to go back to infinity to calculate everything.
Instead of calculating the work needed to move between P and P', it is customary to calculate the work per unit charge in moving from infinity to P and from infinity to P'. That is to say, charge Q1 establishes the field; now we want to calculate
PEelec/Q2 = work/charge = electric potential (V). Thus V = PEelec/Q2 = k Q1/ d where d is the distance from Q1 to the point in question. Electric potential is thus defined as the work per unit charge necessary to bring a charge from infinity to some point in question. Points at different distances from Q1 are at different potentials. We can thus describe the potential difference between points P and P' as the work needed to move a a unit of charge from P to P'. In conventional SI units, work per unit charge would be Joule/Coulomb. We choose to rename this unit 1 volt. See these web sites for other descriptions of electric potential.
http://www.sasked.gov.sk.ca/docs/physics/u3b23phy.html
http://library.advanced.org/10784/phys4.html
http://webug.physics.uiuc.edu/courses/phys112/summer97/lectures/lect06/tsld014.htm
http://www.astro.virginia.edu/~eww6n/physics/ElectricPotentialEnergy.html
Last edited 12/24/05