Iron bearing rocks known as lodestones were known
to early civilizations to have the property of attracting, and
being attracted to, iron implements. Many of these lodestones
were discovered in a territory in Asia minor known as Magnesia,
from which of course we get the word magnet. Besides the property
of attracting iron, an interesting feature of lodestones shaped
into thin needles is that they always orient themselves in a north-south
direction. References to the magnetic compass can be found in
very early eastern writings; similar references appeared in the
west sometime during the twelfth century.
The first formal, thorough study of magnets was done by Sir William
Gilbert at the turn of the 17th century. When not engaging in
his duties as court physician to Queen Elizabeth I, Gilbert carried
out basic research on the nature of the Earth's magnetic field.
He suggested in his book, de Magnete, that the Earth was
a giant lodestone with a field strong enough to cause a compass
needle to be deflected.
See this applet http://www.technical.com/magnetism.html
While electric fields
arise from stationary charges, magnetic fields arise from charges
in motion, either by spinning on an
axis, or by moving along a line. Electrons in atoms spin as they
orbit their nuclei. For most elements, the magnetic fields caused
by the spin of some of the electron population are canceled by
the fields of electrons spinning in the opposite direction. For
three elements, iron, cobalt and nickel, some of the spinning
electrons are unpaired, giving each atom a residual magnetic effect.
These atoms try to line up into ferromagnetic domains so that
their magnetic fields add. This process is hampered by the vibration
of atoms due to thermal effects. However, these tiny domains can
be made to align themselves when placed in a strong magnetic field.
When this happens, an ordinary piece of iron becomes a very strong
magnet. Ironically (pun intended), because we cannot turn
them on or off or otherwise control them, natural magnets get
relatively little attention in physics
For a discussion of the earth as a magnet,
go to
The Exploration of the Earth's Magnetosphere
http://www-spof.gsfc.nasa.gov/Education/Intro.html
Electromagnets
The first connection between electricity
and magnetism was made by the Danish physicist, Hans Christian
Oersted. In 1820, he announced that surrounding a current carrying
wire was a magnetic field strong enough to deflect a compass needle.
Further, he showed that the field direction depended on current
direction in the wire and that a compass placed near a wire carrying
a current would line up tangent to a circle that had the wire
at its center. This discovery caused other scientists to shift
their attention from what was happening inside the wire to what
was happening outside the wire.
Magnetic field strength (B) about a current carrying wire is a
vector quantity given by the equation
|
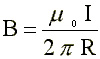 |
see the applet at http://www.walter-fendt.de/ph14e/mfwire.htm
where I is the magnitude of the current
and R is the distance from the wire to the point in question.
There is also a constant involved, uo ( also known as the permeability
of free space) uo = 4 pi x 10^-7 Tm/A The are several units that
are used for B. The SI unit is the Tesla (T) which is equivalent
to a N/A-m. Also, 1 T = 10^4 Gauss = 1 Weber/m^2 = 10^4 Maxwell/cm^2.
(These last units are very out-of-vogue and are seen only in old
text books.)
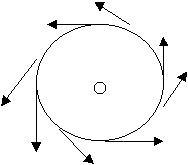
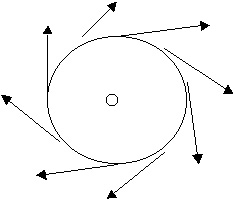
The direction of the B field is very curious. Whereas the field
lines around a stationary charge radiate outward (positive charge)
or inward (negative charge) as the spokes of a wheel, the field
lines around a long straight conductor carrying a current are
set up tangent to a circle that has the wire at the center. There
are two possibilities for a directed line segment to be shown
this way. A way to remember which way nature works is to apply
a version of the right hand rule for determining the directions
of B-fields. Please understand that the direction of a particular
magnetic has nothing to do with your hand; it is just a "handy"
way to remember.The
right hand rule says "Grab the wire with your right hand,
thumb pointing in the direction of the current. Your fingers will
wrap around the wire in the same sense as the magnetic field.
Note that we said "sense"
(clockwise or counter-clockwise) as opposed to same direction
, say due north. See the box below.
|
Right Hand Rule Grasp the wire with your right hand so that your thumb points in the direction of the current. Your fingers will wrap around the wire in the same sense as B. |
|
|
| current out of page | current into page |
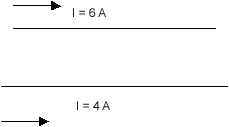 |
See the diagram at left. Consider two
long straight parallel wires 10 cm apart and carrying currents
of 6 A (top) and 4 A (bottom) in the same direction..Find Bnet
A) 5 cm above the top wire; B) 5 cm below the bottom wire; C)
midway between the wires; D) Find the point(s) where B net =
0. what happens here? What happens to these answers if the currents are oppositely directed? |
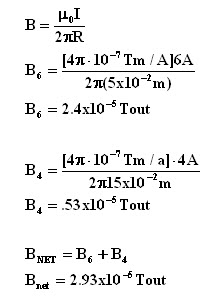 |
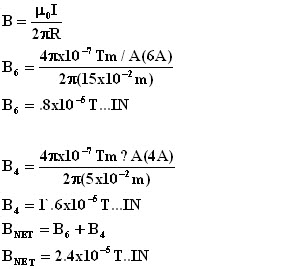 |
 |
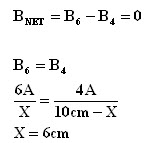
|
| This is the solution to part A | This is the solution to part B | This is the solution to part C | This is the solution to part D |
|
|
|
 |
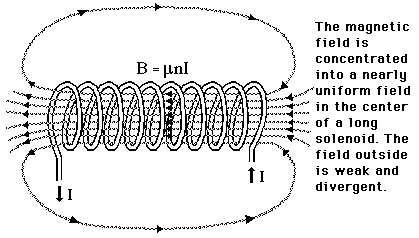 |
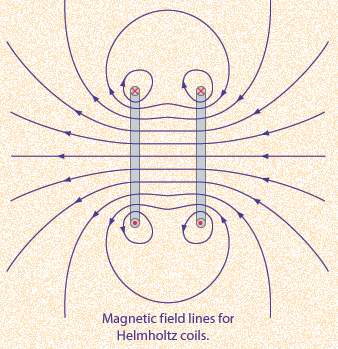
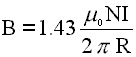 The magnitude of the B-field falls off quickly as we move away from the wire. We find that if we turn the wire into a loop, the center of the loop is equidistant from the wire and the B-field is constant near the center. Add more (N) turns of wire and B is multiplied by N. A special arrangement of two identical coils of some radius R and separated by that same distance R are known as Helmholtz coils. See the figure. |
A second coil called a solenoid consists of many (N) turns of wire wrapped around a long, narrow cylinder. The B-field inside is very nearly uniform everywhere inside the coil except near the ends. |
The applications of the magnetic field to generate electric current,
to transport it efficiently over great distances, and then turn
it to mechanical energy represent one of the great stories in
the history of the development of civilization. We shall look
at these applications in the next chapter on Electrodynamics.
See these Applets
Induced current in a coil
http://www.phys.hawaii.edu/~teb/optics/java/indcur/index.html
The Lorentz Equation
we have already seen that an electric field can propel
a charged particle regardless if it is at rest or moving. This
is not the case with a magnetic field. A magnet will neither attract
nor repel a static charged particle; a magnet will exert a force
on a moving charge, but only if the particle is moving across
field lines rather than parallel to them. We determine empirically
that the force acting on moving charged particles is given by
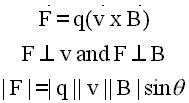
|
the magnitude of the force ia given by the
bottom line in the box.
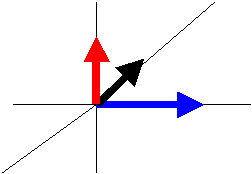 |
The direction of the force is a vector perpendicular to the plane formed by v and B as guided by a different right hand rule which states, for positive charge carriers;1) point your right thumb in the direction of the first vector mentioned (v) on the right-hand side; 2) point your right index finger in the direction of the second vector mentioned (B); the direction of the resultant vector (F) is perperdicular to the plane formed by V abd B and points in the direction of the middle finger of the right hand. Notes: 2) Notice that the vector cross product is not commutative; the magnitude of the vectors is the same, but the direction of the resultant is different. Show that v x B is not equal to B x v. (Magnitude is the same; direction is different.) 3) Note that if the charge carrier is negative, a left hand rule must be applied. That makes a magnetic field a very useful mechanism for separating a beam of mixed (read: positive and negative) charges |
A
variation on the Lorentz equation is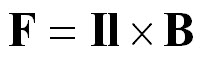 Consider the two wires 10 cm apart seen earlier. |
 |
|
The lower wire creates a B-field which points out of the page at the site of the upper wire. Because the upper wire carries a current, the field from the lower wire exerts a force on the upper wire. The magnitude of this force is F = IlBsin theta (theta is the angle between the current direction and the B-field.). The direction of the force is given by a right-hand rule. Thumb poits in the direction of the current. Index finger points in the direction of B. Convince yourself that the force vector points down. But wait!!! The upper wire carries a current which creates a field at the site of the lower wire. This field points into the page and the force it creates points up. But you knew this would happen because of Newton's third law. |
|
See the excellent applets at these sites.
Note that Internet Explorer may not allow you to view these applets.
We suggest viewing them with a Netscape browser.
http://www.phys.hawaii.edu/~teb/optics/java/partmagn/index.html
See the Lorentz force act on a wire at
http://www.walter-fendt.de/ph14e/lorentzforce.htm
Go to this site and proceed through Prof.
Hershfeld's slides
http://www.phys.ufl.edu/~phy3054/magnet/mfield/Welcome.html
Go to magnetic field problems
Thhis page was last reviewed 03/02/09