Consider the situation above where two objects whose masses are M1 and M2 are moving toward each other with uniform speeds, V1 and V2 respectively, in collinear paths. The objects collide and subsequently separate (or not) with velocities V1' and V2'. One can engage Newton's second and third laws and apply reasoning shown at left. m1v1 represents the momentum of block 1 before the collision; m2v2, the same for block 2. Together the right-hand sum represents the total momentum before the collision. Similar statements on the left-hand side seem to identify all of the momentum in the system after the collision.The statement presented above suggests that in this event momentum is conserved, that is to say, the momentum that exists in the system after the collision is equal to the momentum in the system before the collision. Like the other laws in nature, this one is only good until some experiment shows that it is not valid. To date, none has been found and the law of conservation of momentum represents one of the fundamental rules at the heart of physics.

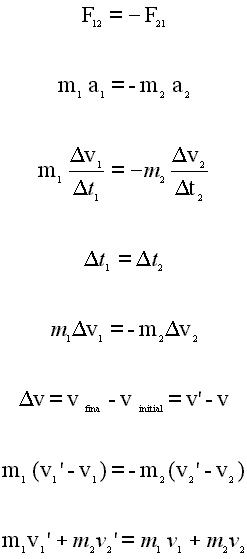See this wonderful applet
http://www.lon-capa.org/~mmp/kap6/cd157a.htm

INELASTIC INTERACTIONS

Most interactions between objects are said t be Inelastic wherein momentum is conserved, but not kinetic energy. Note that this is not a violation of the law of conservation of energy. In inelasatic events, some KE may be converted to heat. KE is considered "lost" not because we cannot find it but rather because we cannot retrieve it. Examples of inelastic events include moving objects colliding and sticking together, or two objects moving (or not) and springing apart. A quick calculation of KE before and after the event will confirm this. We can account for the missing energy; we just cannot get to it easily.

Sometimes the question is phrased "what fraction of the original KE is lost?" The answer to this question involves building a fraction that has a numerator and a denominator. The syntax of the question can be used as a guide building this fraction. What follows the word "of" in the question goes into the denominator; what follows the word "is"goes to the numerator. As an example, what fraction of 4 is 3? "What fraction of the original kinetic energy is lost?"becomes a fraction (KE before - KE after) / KE before. While this fraction seems ungainly, substituting masses and velocities often yield a very managab,e answer

Visit this applet to see the law at work
http://zebu.uoregon.edu/nsf/mo.html

ELASTIC COLLISIONS

The law of conservation of momemtum applies in all interactions (collisions and explosions) in one, two, or three dimensions (all means all). Additionally, If the proper circumstances are in place, a collision can occur where kinetic energy as well as momentum is conserved. Such a collision is elastic If such an event takes place, two other equations apply and are presented below. If objects M1 and M2 move with velocities V1 & V2, respectively, before the elastic collision, then the velocities of objects after the collision are given by

the

For a derivation of these equations, click here

It is common (though not absolutely necessary) when using these equations to let V2 = zero. This allows the reader to focus attention on each object before and after the collision.

• Case 1 m1 = m2 (the classic billiard ball collision) The cue ball M1 moves with speed v1, strikes the object ball (m2, initially at rest) sharply and without spin. What does your intuition tell you about v1' and v2'? Test the validity of your intuition by letting m1 = m2 in this collision.
• Case 2: m1> m2 (massive golf club head striking a ball). let m1 > m2. How do v1' and v2' each compare with v1? In particular, what happens to v2 ' as M1 increases? What is the largest value that v2' can have?
• Case 3:m1< m2 (marble strikes a bowling ball

Check out these web sites.

HYPERPHYSICS

M 31	http://tqd.advanced.org/3042/java/linear_demo.html
M 32	http://www.mcasco.com/p1lmc.html http://www.sasked.gov.sk.ca/docs/physics/u5a23phy.html http://schutz.ucsc.edu/~josh/5A/book/momentum/node7.html http://theory.uwinnipeg.ca/physics/mom/node3.html http://library.advanced.org/16600/intermediate/momentum.shtml
M 33	For another look at collisions go to http://rip.physics.unk.edu/CyberTextBook/Collision/ Try these applets to test the law of conservation of momentum http://zebu.uoregon.edu/nsf/mo.html http://www.phy.ntnu.edu.tw/~hwang/billiards/billiards.html

A hallmark of mechanics is the consideration of word problems. Useful relationships are published here in a page called EQUATIONS. The reader should consult this page before attempting the problems assigned.

Go to homework problems
Go to problems at U Oregon
http://www.zebu.uoregon.edu/~probs/mech/collid.html

Return to Conservation Laws

 This page was last reviewed 10/16/05