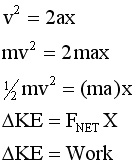The person responsible for the law of conservation of energy is James Prescott Joule, for whom the SI unit of energy is named. Joule worked in the family brewery and became interested in reducing the waste heat in the brewing process. Before he had finished his work, he had determined the mechanical equivalent of heat.; that is, there is a definite numerical connection between mechanical energy dumped into a system and heat energy removed from the system, and conversely. In modern terms, 4.185 Joules of mechanical energy equals one calorie of heat energy.

These sites pertain to biographical data about JP Joule. http://physics.hallym.ac.kr/reference/physicist/joule.htm http://www.answersingenesis.org/docs/3277.asp

Work & Energy
It is useful to define a quantity called work. 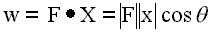. This form is formally known as the scalar product of two vectors but is also commonly known as the dot product. We can define work as the product of a force acting through a distance. It is important to note that while F and X are vectors, W is a scalar. Furthermore, by convention, the dot product operator causes the magnitude of W to be W = |F| |x| cos q, where q is the angle between F and x. In most applications the force and the distance through which the force acts are collinear and pointed in the same direction; q = 0 and the cos 0 = 1. Things get a little tricky when a force is applied to an object that is moving some distance in a direction perpendicular to the force. In this situation the angle q between F and x is 90, the cos 90 = 0 and the force does no work.
The unit for work is the Nm (Newton-meter) which is renamed the Joule in honor of the man.

A useful applet on the scalar product of two vectors can be seen at
http://www.lon-capa.org/~mmp/kap17/scalar/scalar.htm

Kinetic energy
What happens to the work done if I throw a ball. I exert a force F( assumed constant in magnitude for this argument) through some distance x in the wind up and delivery. Thus I do work such that W = F X . Check out the derivation in the box

Our work in kinematics suggests that if the ball starts from rest (initially at wind up), equation 4 (page 1) yields
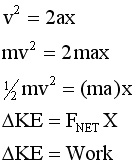Multiply both sides of the equation by m (mass) and by 1/2
Kinetic energy is given by the expression 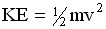, where m is the mass of the object and v is its speed.
The units for KE are equivalent to units for work.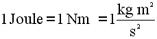

The fact that the expression for kinetic energy shows the speed of the object squared is significant. At any given speed for an automobile, doubling the speed means increasing its Kinetic Energy by 2 squared = 4; the engine has to work four times harder. And if stopping a car at a given speed takes a given distance X, then the stopping distance from the doubled speed means 4 times the stopping distance.

Gravitational potential energy
We can do work on a block to lift it to some high place. At the end of the trip, we have done work in moving the block but the kinetic energy of the block is zero at the upper location. If we release the block, it falls toward the floor and has acquired kinetic energy just before hitting the floor. Where did that energy come from?

We say that the work done in lifting the block was stored in the Earth's gravitational field and was retrieved when the block was released. Close to the surface of the Earth, gravitational potential energy is given by PEg = mgh, where h is the height through which the block was raised and g is taken as a constant 9.8 m/s/s for the entire distance h.

PEg manifests itself as the energy a) stored behind the dam at a hydropower station; b) stored in counter weights in elevators or in older double-hung windows (the ones with sash cords); c) stored in counterweights in some grandfather clocks.

Elastic potential energy
It is possible to apply a stressing force to a spring to stretch or compress it some distance. It is our common experience that the spring will return to its original rest position when the stressing force is removed. Robert Hooke, Newton's venerable nemesis, determined the force needed to stretch a spring some distance is not a constant but varies directly with the distance stretched. We can write this as F = kx. k is called the force constant (units: N/m) and is constant over a relatively short span of compression or extension. If the object is stretched beyond a point called the elastic limit, Hooke's law no longer prevails. Ever stretch the spring of a retractable ball point pen too far? What once passed for a spring becomes a twisted piece of wire.

Body builders who need an alternative to lifting weights will often stretch springs. Larger values of k mean that it will take a large force to stretch the spring a small distance

In applying a force acting through a distance, we have done work on the system. Where did it go? We say that the work done is stored in the spring as elastic potential eneregy and can be retrieved when the spring is released. Because the force varies from zero to some large number, we must average the initial and final forces. W = 1/2 (F + 0) x. = 1/2 (kx + 0) x. PEelas = 1/2 k x².

You can find elastic PE ready to work for you in the following applications: the springs in mouse traps and in wind up toys and non-battery wrist watches, the bend in a pole vaulter's fiber glass pole.

We need to add here that non-conservative forces such as friction may act on the object as it moves and convert its mechanical energy to heat. The reader must understand that the conservation law is still intact. Friction has simply made the energy irretrievable for any mechanical purpose.

http://www.dti.gov.uk/renewable/ed_pack/games/12-16/
http://www.st-agnes.org/~lstinson/webpages/kinpot.htm

This site shows an interactive, animated version of a car negotiating first a hill, then a loop

http://www.funderstanding.com/k12/coaster/

http://www.suite101.com/article.cfm/12/54640
This site under the title "Angular Momentum: The
Counter-Intuitive Conservation Law" includes information relating to how
orientation affects the conservation of energy, different definitions for
terms relating to the conservation of energy.

This site claims to be an online classroom containing
all the basics such as termonology of Potential
Energy, Kenitic Energy, Mechanical Energy and Power.
There are pictures and easy to understand
descriptions.

http://www.phys.virginia.edu/classes/581/MostlyPE.html

Summary of the work energy business. Obviously comes
from the University of Virginia (reliable site).

M 37	Visit  HYPERPHYSICS    and check out this topic.
M 38	http://www.mcasco.com/p1wke.html http://www.mcasco.com/p1pef.html

And what if the conservation laws did not always prevail? The result would be perpetual motion machines.

A famous example of such a device is "Waterfall" by M.C, Escher shown at left. What's wrong with this picture?

A hallmark of Mechanics is the consideration of word problems. Useful relationships are published here in a page called EQUATIONS. The reader should consult this page before attempting the problems assigned.

Go to supplementary problems - energy

Go to problems at U Oregon
http://zebu.uoregon.edu/~dmason/probs/mech/work.html

Does the object that travels the shorter distance win the race?- Try the racing balls applet
http://www.phy.ntnu.edu.tw/~hwang/racingBall/racingBall.html

Return to Top

Return to Mechanics

Page last modified 11/25/05