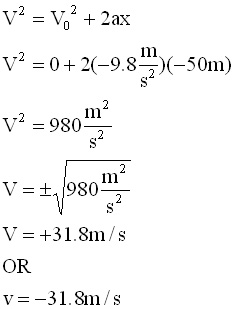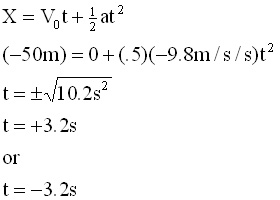The early Greeks, Aristotle in particular, had opinions on most everything, including how things move. In their view of the universe there were four elements: earth, water, air and fire. If an object made of earth was displaced out of its natural location, the "natural motion" of the object would cause it to be returned to earth through water and air. Similarly, an upside-down bucket pushed into the water trapping air will allow the air to be released to its natural location when the bucket is turned upright. They also believed that an object when released would quickly attain its natural velocity and would fall at that rate until it hit the ground.
		The explanation of falling bodies by the Greeks prevailed until nearly the middle of the 17th-century when Galileo, a mathematician from Venice, published his Dialogue Concerning Two New World Systems in 1636. It is in this book published after the trial for heresy in 1633 that he reveals his findings of extensive experiments involving falling bodies and balls rolling down inclined planes. His work closely resembles the modern view of how things fall, a conclusion made remarkable when one considers that he did not have an easy way of measuring time. There were no mechanical clocks in his time. He relied first on the water clock and later a pendulum to measure time.Galileo concluded from his experiments that objects starting from rest would move faster and faster as they fell. Furthermore, he suggested that the rate of increase in velocity was well behaved and mathematical. He found that if an object fell one unit of distance in one unit of time, then during a second unit of time it would fall three more units of distance, during a third unit of time five more units of distance, etc. He also suggested that the air provided opposition to free fall, with air drag having greater influence on lighter objects than heavier ones. He suggested that if a space could be evacuated of air, a coin and a feather should fall to Earth side by side.While this last assertion would need 200 years and more before it was proven, the mathematics of falling bodies showed up in the work of Isaac Newton.

A second kind of motion in one direction is the vertical motion that occurs in the Earth’s gravitational field. If I hold a stone at arm’s length and release it, its velocity is initially zero. Moments later as it is falling, its velocity is not zero. Therefore the stone has undergone a change in velocity during a change in time, the definition of acceleration; we call this the acceleration due to gravity (rather than the acceleration of gravity). On this planet g = 9.80 m/s/s at most common locations. (Why it is this value will become evident in the dynamics section of the course.)

Perhaps our first order of business should be to alter our sign convention to read:

Any vector pointing up is positive; any vector pointing down is negative.

We measure displacements from the starting point of the trip to the stopping point of the trip.

For a body thrown upward, the initial velocity shall mean the velocity at the instant it has left the thrower’s hand.

For a body moving downward, we will take final velocity to mean the velocity at the instant before the body hits the ground.

The force of gravity, and therefore the acceleration due to gravity, always points down.
Therefore by our convention g = - 9.8 m/s /s.

We wish to call the quantity in question ACceleration and not DEceleration. Thus, an object launched upward initially has a positive velocity. For each second that it moves, we add -9.8 m/s to its velocity. At some point in time the velocity goes to zero--the object stops. Gravity continues to add -9.8 m/s to the velocity, making that quantity negative--the ball is coming down. The reader should note carefully that during the upward part of the trip, the negative acceleration causes the object to slow down and stop. As time marches on, the acceleration is still negative and the object speeds up as it falls back to Earth.

Problem 1.2.1 A ball is dropped from a balcony and falls 50 m to the ground. Determine a) the flight time and b) the velocity at impact.
GIVEN THAT vo = 0 a = g = -9.8 m/s/s x = -50 m FIND V & T	Finding V Use equation page, 1 line 4
The ball is moving downward when it hits the ground. The correct answer is -31.8 m/s. The positive solution is extraneous
The correct answer for t is positive because it is a scalar.

See also

Remote Reading Assignments
HYPERPHYSICS	GLENBROOK HS	M CASCO & ASSOCIATES

Homework Problems
361

Return to kinematics

Return to mechanics

---