Elevator down     A more complicated motion than those described above occurs when an object is projected with a velocity component at right angles to the downward force of gravity. In this first encounter with projectile motion, we consider situations where there are no forces such as air resistance acting horizontally on the object. When such simple conditions exist, the motion of the projectile can be derived and described in terms of the relationships found on page three of EQUATIONS. as well as in the boxes below. These equations tie together velocity components as a function of time, as well as position in the x-y plane as a function of time. Along the way, we will be able to demonstrate that the path of a projectile launched under these conditions is parabolic. At this entry level of consideration, the factors that determine the path of a projectile as it flies through the air are: the velocity of projection Vo, the angle of projection (theta), and the local value of g. (Missing from this list is air resistance.) Let's look at the equations in the boxes below. .  line1 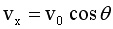  Given Vo, g, and theta, lines 1 & 2 yield the horizontal and vertical components of the projectile velocity as a function of time.  line 2    line 3    Given Vo, g and theta, If we know how long the object has been in flight, the equations known as lines 3 & 4 will yield a displacement horizontally and vertically as measured from the point of projection. .  line 4    line 5   The given suggest that of all the bizillions of points in the plane, a small population are occupied by the projectile and will fit a curve that is line 5.  line 6    If the launch angle is zero, (necessarily,this occurs from a cliff or table top, etc.), line 5 reduces to line 6.  line 7       If the landing place is at the same level at the point of projection, then the landing place is (R, 0) where R is called horizontal range and falls out as line 7    Let us try a series of launches. In each case we place a pair of coordinate axes (in red) and an indicated the general direction of the projectile We will assume g = 9.8 m/s/s and that there is no air resistance   Case 1 Projectile is launched at 5 m/s @ 30 degrees and lands on level ground Projectile will land at (X, 0). Use line 7    Case 2 Projectile is launched at 5 m/s @ 30 degrees and lands 10 m below level ground  Projectile will land at (X, -10). Use line 5   Case 3 Projectile is launched at 5 m/s @ zero degrees and lands 10 m below level ground  Line six works here   Case 4 Projectile is launched at 5 m/s @ 30 degrees above and lands on a 7 degree slope. [Hint: The path of the projectile will follow a course given by line 5 with an angle of 37deg. We are looking for the point where this curve intersects y = x tan 7]       Remote Reading Assignments  HYPERPHYSICS  GLENBROOK HS See lesson 2  M CASCO & ASSOCIATES  BLOOMFIELD - HOW THINGS WORK Projectile motion is a topic that lends itself to applets very nicely.Give these careful attention. Please note that some of these applets will not play on Internet Explorer; fortunately, they can be used with Netscape as a browser.  M - 43  Go target shooting with this applet. http://zebu.uoregon.edu/nsf/cannon.html One way to treat this applet is to fire a round and see where it lands. The artillery term for this is"fire for effect" and reduces the applet to a primitive video game. You have better games at home; let's put this applet to more serious purpose 1. Install a coordinate system with the origin at the point of projection. There is a built in ruler to help measure distances. Using this ruler, determine the x-y address of the center of the target. 2. See the equation (page three line 5). You are given default launch parameters for velocity, angle of projection, and local gravity. If the shell is to hit the target, then when x = your x-address, y = your y address. Solve for y and see if it fits your y address. Fire for effect to confirm your calculation. 3. We need to hit the target. Go back to the equation (p3, l5), given the default values for angle and g, LET x and y be your x-y address, solve for the velocity. Set the velocity for this value and fire for effect. What happened? 4. If the x-y address of the target were (X, 0), something interesting occurs: if you can hit the target on the first shot with a given set of launch parameters, then you can hit it with the second shot by setting the launch angle equal to the complement of the first angle. Try it.    This applet allows you to test the famous "monkey in the tree" demonstration. A hunter wishes to shoot at a monkey in a tree using a very primitive rifle that has no sighting device. He simply aims at the monkey and pulls the trigger. It seems that the monkey has his own theory about how this will work..He thinks that the bullet will travel a straight line path to his perch in the tree; therefore, as soon as he sees the flash from the gun, he lets go of the branch and hopes to falls out of harm's way. See the action at http://jersey.uoregon.edu/vlab/newCannon/NewCannon_plugin.html For a live demonstration of this experiment, click here to go to the University of Minnesota. Scroll down to The monkey   It will take a few seconds for this applet to load  Our friends at Glenbrook display an applet of a cannon ball fired horizontally from the edge of a cliff. Pay careful attention to the horizontal and vertical components of the velocity vector. The horizontal component remains the same but the vertical component increases as time marches on. See the applet at http://www.glenbrook.k12.il.us/gbssci/phys/mmedia/vectors/hlp.html  This applet calculates range, height and time of flight as you manipulate the velocity and angle of projection. In a football game, the punter tries to get the ball as far down the field as possible while keeping it in the air as long as possible. What angle will yield the maximum value for range? For hang time? What is a good compromise for both of these quantities on the same kick? See the applet at http://www.phys.virginia.edu/classes/109N/more_stuff/Applets/ProjectileMotion/jarapplet.html  Like the previous applet, this one allows you to set parameters for angle of projection and launch velocity and stores on screen the data for 6-7 shots. See the applet at http://www.msu.edu/user/brechtjo/physics/cannon/cannon.html  Launch a projectile horizontally from an elevated plateau and it will follow a parabolic path to the ground. The same projectile launched with a larger velocity travels further before the ground. What happens to the path of the projectile if it is launched so fast that Earth curves away from it before it gets there. At that very special velocity (which will calculate later on) the object is said to be in orbit. See the applet at http://www.phys.virginia.edu/classes/109N/more_stuff/Applets/newt/newtmtn.html Here is a lab activity for this topic. For plans on how to build a trebuchet go to http://www.fryerskits.demon.co.uk/treb  368 361   Return to kinematics This page last edited 01/23/09