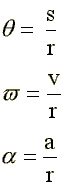Rotational Kinematics

A common motion that deserves our attention is that of a object that stays in place but spins on an axis. Whereas in an earlier section of this course we dealt with linear motion in a straight line (this is called translational motion), now we deal with rotational motion (a.k.a. angular motion).
For a disk rotating at a uniform rate about its axis, every point on the disk has the same angular displacement theta that is, each point moves through the same angle. The unit of angle for this section is the radian.

 If we measure the time it takes to move through an angle, we can determine the angular velocity w (symbol is w omega), measured in rad/s. Again, if the angular velocity of an object changes during some amount of time, we can determine the angular acceleration a measured in rad/s/s (a symbol is alpha).
Of particular interest to us is the relationship between the angular velocity of a rotating object and the linear velocity of point on its surface. Consider the Earth. Every point on the planet rotates through 2 p radians in 24 hours, about a quarter of a radian/hr. Not every point on the surface has the same linear velocity. The relationship between them is v = (r) (w). Hence, the further out from the center of rotation is some point, the larger is its linear velocity. Can you determine the linear velocity of some point on the equator? What is the linear velocity for Waterville (latitude 44.5 degrees)?

Visit these web sites for additional explanation of this topic.

http://www.mcasco.com/p1rot.html

The statements at the immediate right address the determination of the magnitude of angular displacement, angular veloccity and angular axxeleration.  At far right are equations that are to rotary motion what page 1  equations are to motion j n one dimension

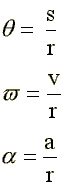
For a first view of what causes things to rotate the way they do, see
http://www.mcasco.com/p1rdy.html

Go tp problems at U Oregon
http://www.zebu.uoregon.edu/~probs/mech/circ.html

Return to mechanics

This page last edited 01/23/09.