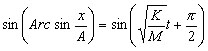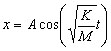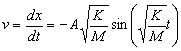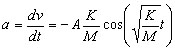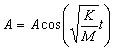|
SIMPLE
HARMONIC MOTION
Perhaps the most complicated
motion we will study in a high school mechanics course is simple
harmonic motion (SHM, for short). Harmonic motion implies that
the object is moving through some pattern or path during a given
period of time. the object then repeats, or tries to repeat,
this path during the next equal period of time. More complicated
harmonic oscillators are compound oscillators involving multiple
moving objects, or an object with multiple moving parts, such
as musical instruments, and damped harmonic oscillators such
as automobile springs with shock absorbers attached.
The usual example of a simple harmonic oscillator is the simple
pendulum, a mass of significant size attached to a string of
negligible mass which in turn is attached to a friction-free
support. History shows that Galileo was the first to show that
the pendulum kept time as it repeated its motion again and again;
the pendulums in question were incense pots swung from chains
attached to the ceilings of churches. He measured the time it
took for one cycle against his pulse (remember, he was trained
as a physician). For a brief discussion of Galileo's role in
the pendulum as a timer, go to http://es.rice.edu/ES/humsoc/Galileo/Student_Work/Experiment95/galileo_pendulum.html
A companion example of SHM
involves a block of known mass attached to a massless spring
whose constant is k and which loses no energy in flexing the
spring. It is common for the spring and block to be moving horizontally,
so that gravity acts on all parts of the object in the same way.
In either case, it is important to learn where equilibrium is
located for the object. It is at this place where Fnet equals
zero.When a force of sufficient size is applied to the object,
the object is displaced out of equilibrium. When released, some
force (gravity for the pendulum, the Hooke's law force for the
spring) causes the object to return to the equilibrium position.
For this reason, regardless of what other name this force has,
it is also called a restoring force. It happens that the greater
the displacement from equilibrium, the greater will be the restoring
force. That means that the acceleration of the object in question
is not uniform; we cannot use page one equations to solve for
position or velocity or whatever. Additionally, as the acceleration
goes to zero during a cycle, the speed increases to its maximum
value. Conversely, as the acceleration vector increases, the
velocity vector goes to zero.
Herewith is a derivation of
the relationships in questionSimple Harmonic motion
Consider a block of mass M a resting
on a horizontal, friction-free surface. One end of a coil spring
is attached to the block; the other end of the spring is attached
to the wall. If the block is pulled to one side and released,
the force of the spring will be the only force acting on it in
the x direction in the object will accelerate in the x- direction.
(A net force in the y-direction is 0and these forces will not
become a factor in this problem)
What we would like to do is displace the block from its equilibrium
position and release the block. We would like to know relationships
for position-, velocity-, acceleration of this block was a function
of time as well as the velocity of the block as a function of
position. |
|
The law of conservation of energy
suggests that the energy stored in the spring at maximum comprression
(or extension) manifests itself as potential or kinetic energy
whenever the block is somewhere between these two extreme points |
line 1 |
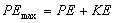 |
|
Line one is expanded here.
"A" in this equation is amplitude, defined as the maximum
dslacement. |
2 |
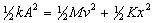 |
|
Solve line 2 for v (you
can do this). This equation yields velocity as a function of
position. Give me initial conditions and tell me where the object
is and I can determine how fast the block is moving. This is
analogous to an earlier kinematics equation See equations, page
1, line 4. |
3 |
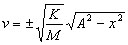 |
|
One way to define velocity
using calculus |
4 |
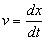 |
|
Substitute line 3 into
line 4 |
5 |
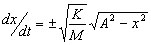 |
Rearrange and prepare to
integrate. I can never remember the trick, See http://www.exambot.com/cgi/reference/
show.cgi/math/intc/mint/inv_trig_sub.ref |
6 |
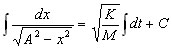 |
|
ta-dah!!! |
7 |
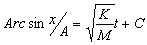 |
|
We need to establish some
initial condition by assigning a value for C. This says we shall
start timing the block when it is farthest to the right |
8 |
Let x = A when T = 0 |
|
the Let statement is consistent
with our initial conditions |
9 |
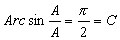 |
|
The "things" on either
side of the equation in line 10 are angles. If two angles are
equal then their sines are equal |
10 |
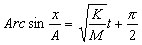 |
line 11 will clean up with an identity.
See
http://www.exambot.com/cgi/reference/show.cgi/math/trigid.ref |
11 |
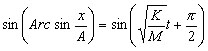 |
|
Here is an equation for position
as a function of time. See page 1, line 3. Take a derivitive
wrt time to get line 13 |
12 |
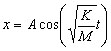 |
A derivative of this line gets to
acceleration.
See page one line 1 |
13 |
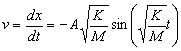 |
|
Line 14 has no equivalent on
page 1. The acceleration is constant there; here it varies witk
time. |
14 |
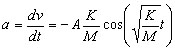 |
|
O |
|
|
|
Line 12 tells us that when
t = 0, X = A. Let us calculate the elapsed time until the next
moment when x = A. Return to line 12. Let x = A |
15 |
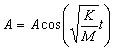 |
In line 15, if x = A, then
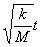 must be an angle whose cosine
= 1. Zero radians is a trivial solution (the block has not moved
yet). The next angle for whihch this is true is 2 pi radians must be an angle whose cosine
= 1. Zero radians is a trivial solution (the block has not moved
yet). The next angle for whihch this is true is 2 pi radians |
16 |
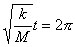 |
Let us solve line 16 for
t and while we are at it, let us rename it T.
This is called period,
the time for one cycle. |
17 |
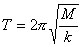 |
|
Line 18 shows a different
arrangement of line 17. The left side is called angular frequency
(unit = 1/s). The left side can be substituted for the right
hand side in lines 12, 13, & 14 above |
18 |
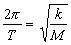 |
|
Note 1. IUsng the equations
in lines 12, 13, 14 above, you can use M and K, or their equivalent
2 pi/ T |
19 |
|
|
Note 2. Let' s say an oscillator
has an amplitude of 20 cm and a period of 4 s. If the block takes
4 s for one cycle, the it should take two s to go from the far
right (x = A) to the far left (x = - A). And if it takes 2 s
to go from X = a to x = -A, then it should take 1 s to go from
X = +A to x = 0. . |
20 |
|
Note 3. Calculate x, v
and A when T = .5 s.
x should be positive (rhs of equlibrium)
v should be negative (it is moving left)
a should be positive |
|
|
Note 3 stated differrently:
if one cycle can be broken into 4 distinct parts, then
x is positive in quads 1 & 4
v is positive in quads 3 & 4
a is positive in quads 2 & 3 |
|
|
|
|
|
|
THE
SIMPLE PENDULUM
A simple pendulum consists
of a ball attached to one end of a string, the other end is attached
to a firm, friction-free point. It is important that the mass
of the string is negligible when compared to the mass of the
ball. We find that the period of oscillation
T = 2 pi [sq rt (l/g). The carreful reader will note that this
equation makes no mention of the mass of the ball or of the size
of the initial displacement.
pendulum applets
http://www.phys.hawaii.edu/~teb/java/ntnujava/Pendulum/Pendulum.html
http://www.nep.chubu.ac.jp/~nepjava/javacode/Furiko_handleEvent/Furiko_handleEvent.html
http://pathfinder.esu2.k12.ne.us/java/physics/physengl/pendulum.htm
http://www.phys.hawaii.edu/~teb/optics/java/pend2/index.html
The site below contains a marvelous description of the topic.
http://www.mcasco.com/p1vib.html
http://webug.physics.uiuc.edu/courses/phys111/fall97/Lectures/Lect25sw/sld001.htm
http://library.advanced.org/16600/intermediate/simpleharmonicmotion.shtml
A hallmark of mechanics is the consideration of word problems.
Useful relationships are published here in a page called EQUATIONS. The reader should
consult this page before attempting the problems assigned.
Go to Supplementary Problems - SHM
SIDEBAR
Psst. Got the time? For a discussion of the pendulum as a timer,
go to
http://physics.nist.gov/GenInt/Time/revol.html
As the world turns.....For
a discussion of the Foucault pendulum, go to
http://www.physics.uoguelph.ca/foucault1.html
http://www.si.edu/resource/faq/nmah/pendulum.htm
This page was last edited 01/24/09
Return
to Mechanics |