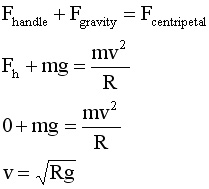Elevator down

Consider an object moving now with uniform speed in a straight line, say in a direction left to right. From Newton's first law, we can conclude that Fnet acting on the object is zero.To make the object speed up, one would apply some additional force pointing right. To cause the object to slow down, the force should be applied to the left (until the object stops anyway). But what will happen if the force is applied to the object at a right angle to its original path? It will neither speed up nor slow down, but rather will change direction. If the force changes its direction so the it always is at right angles to the path of the object, the resulting path will be a circle with the force pointing toward the center of the circle. If the force is constant in magnitude, we call the result uniform circular motion. Thus when we see an object moving is a circular path, we can look to the center of the circle to find the source(s) of the force causing this motion. When Newton considered the path of the moon around the Earth or the paths of the planets around the sun, he was compelled to find some new force holding everything together.

The force(s) add up to Fnet which in this case is called a centripetal force, so named from the Latin roots meaning center-seeking. The acceleration also points toward the center of the circle and takes on the form a_c = v²/R, where R is the radius of the path and v is the speed of the object in question. Thus we consider the motion of an object moving in a circular path at constant speed but is still accelerating. Go back to definitions; 1) acceleration is a change in velocity during some time interval; 2) velocity, because it is a vector quantity, has a magnitude and a direction; therefore a change in direction means the velocity has changed; 3) in earlier circumstances acceleration meant only changes in magnitude; now it can apply to changes in direction.
The word centripetal should not be confused with centrifugal (from the Latin for center-fleeing). Perhaps you have been in an automobile that has rounded a curve slightly too fast. It would appear that your body is flung out away from the center of the circle. In fact, what is happening is that your body, perhaps not firmly ensconced on the car seat, travels with uniform speed in a straight line, while the car slides under you to negotiate the turn.

A Ball at the End of a String

Consider a ball attached to one end of a string; the other end of the string is fixed in place. [Draw a picture.] When the object is at rest, analysis of the ball shows two forces acting on the object--Tension (which points up) and the force of gravity (which points down). T - mg = Fnet = 0. So T = mg. No big deal.

Now we hold the string horizontally so that the ball is at 9 o'clock. When released, the ball starts from rest and accelerates downward along an arced path. [Draw another picture.] What is the tension on the string now?
At six o'clock T - mg = Fnet = mv^2/R. So T = mg + mv^2/R. When v = 0, this equation reduces to T = mg , as suspwcted. We will soon see in the energy unit that the ball released at 9 o'clock reaches 6 o'clock with v = sq rt [2gL]. Substituting this value for v in the preceding sentence, and T = 3 mg. Can you do the math. (What implications does this larger force have on Tarzan as he swings through the jungle.)

If T = 0 when the string is at 9 o'clock and T = 3 mg at 6 o'clock. What is it in between? Careful analysis shows that, for intermediate places along the way, T = mg cos q, where q is the angle the string makes with the vertical. If T = mg cos q, what is T at 6 , 7, 8, & 9 o'clock

CARS & FRICTION

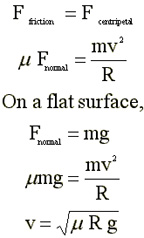In most situations where cars attempt to negotiate turns on the highway, friction is the agent causing the car to move out of the straight line path and into the curve. The bottom line at left shows some of the consideration given to this matter by civil engineers. They will determine what should be the uppermost legal speed on the curve (and add some margin of safety). They will then check to see how large a radius the project can handle. In most of Maine's interstate highway system, land is not an issue and curve radii are very large. . In tight areas, the engineer could also tell the sand and gravel people how gritty to deliver the pavement in order to increase the coefficient of friction For a given curve, if the frictional force is greater than the centripetal force needed, the car makes the turn easily. But if the car is traveling too fast, frictional force is maxed out even under favorable conditions and the curve may prove treacherous. Things get worse if u is reduced by rain. One often sees a sign that reads "Slippery when wet" for that reason.

DETERMINING THE MASS OF THE EARTH (& sun & planets)

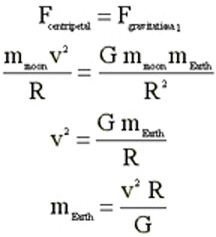Archimedes said "Give me a place to stand and I will move the Earth."Did he know how big a load he was attempting to move? No, he did not. The calculations at left show that we can calculate the mass of the Earth by observing the motion of the moon around the Earth.Is the speed of the moon, determined by v = D/t. D = 2 pi R where R is the Earth-moon distance (known to ancients) and t = lunar period (also known to ancients). The missing piece was supplied by Henry Cavendish who determined G in 1799. This reasoning does not apply to the Earth only. We can determine the mass of any planet that has satellites by applying these rules. The mass of Mercury and Venus are determined by the amount of deviation from its assigned path experienced by the Earth when the planets are close by. Finally, we can determine the mass of the sun by substituting the speed of a planet and the radius of its orbit

DETERMINING THE ORBITAL VELOCITY OF A SATELLITE

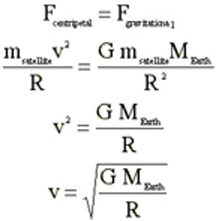Let's now calculate the orbital speed of a satellite placed in orbit around the Earth. .Let's try for a circular orbit where the satellite will be held in place by gravity. How can we do this? The path is not a straight line; it's a circle. Something at the center is acting on the satellite. Calculate v when G = 6.67 x 10^-11 N m^2/s^2 M = 5.98 x 10^24 kg R = 6.38 x 10^6 m

PLACEMENT OF A SATELLITE INTO GEOSYNCHRONOUS ORBIT

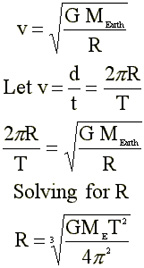The answer to the question in the previous paragraph is v = 7906 m/s = 17, 686 mi/hr. That means that the satellite orbits the Earth once every 85 minutes. If the device is a communication satellite, it is only in a position favorable for broadcast about 15 minutes per orbit. Telstar, launched in 1963, functioned this way. By modern standards, this is a useless orbit. Instead, we want a satellite that is always overhead, always ready to receive and resend. Such a satellite is said to be in geosynchronous orbit.and will maintain a position over the equator if its position and speed are preset. Solve the equation at bottom left for R to get the proper location of a modern communication satellite. Place the value of R in the previous box and get the proper orbital velocity

Usually, the object under early consideration in a physics course is moving in a circle that lies in a plane parallel to the ground. In this way, gravity acts on all parts of the path in the same way and the acceleration of the object is usually unchanging in magnitude. For objects moving in a vertical circle, gravity causes the acceleration to vary moment to moment. We will defer consideration of motion in a vertical circle until we have developed the idea of energy; this will make our work easier.

One question that we can answer without resorting to energy considerations is this: If a pail of water is whirled in a vertical circle, what minimum speed must it have at 12 o'clock to ensure that it completes the circle without spilling. See the solution in the box below.

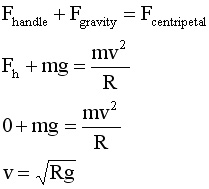
Consider a pail of water swung in a vertical circle. How slow can it move at 12 o'clock (its highest point) without spilling the water. At 12 o'clock, the forces acting on the pail are gravity and the handle which combine to provide the centripetal force that must be present to cause the circular path. See line 2. If the pail were whirled faster, v squared would increase, so too would the right hand side. If the equation is to hold together, the left side must increase by the same amount. mg cannot increase; the handle must supply all of the additional force. Instead of going faster, let's slow down the pail of water. As v is decreased, mg is still fixed; the only variable that can change is F handle which can go to zero. See line 3. Solve for v. See line 4.

Because motion in a circular path is not immediately clear to everyone, there are many web sites posted by persons who wish to take a turn at explaining what is happening. Here are some of the better tries.

	These remote reading sites have been chosen for your attention as you prepare Electronic Summaries
	http://www.mcasco.com/p1cmot.html
	http://webphysics.ph.msstate.edu/jc/library/5-1/index.html
	http://www.glenbrook.k12.il.us/gbssci/phys/mmedia/circmot/ucm.html
	http://www.sasked.gov.sk.ca/docs/physics/u5d3phy.html

Return to Newton's Laws