Elevator down In an earlier lesson we defined displacement as the straight-line distance from the start of a trip to the end of a trip. Adding displacements is rather straightforward when motion occurs in one dimension. If we represent vectors as directed line segments (arrows), we can represent vector addition by linking the arrows head to tail. The vector sum (known in some circles as the resultant) is that arrow drawn from the tail of the first vector to the head of the last vector in the addition sequence. A displacement of 4 units right plus a displacement of 3 units right adds to 7 units right. See figure 1. Similarly, 4 units right plus 3 units left adds to 1 unit right. See figure 2. Please note that the addition of vectors is commutative; one would arrive at the same end point even if the order of operation were reversed.          Figure 1   Figure 2   Figure 3   Figure 4 The plot thickens (see figure 3) when we consider motion in two dimensions. Four units right plus 3 units up in fact adds to 5 units (thank you, Mr. Pythagorus) at an angle (close to 37o, actually) that points up and to the right. Sadly, that's where the easy math ends.When vectors in two dimensions are not perpendicular, we are forced to apply other mathematical means to solve the problem. (see figure 5.) It shows a vector (in black) pointing up and to the right. We have broken the vector into two parts--a component that points right (red dashed line) and a component that points up.. (blue dashed line) This process is called the resolution of a vector. We have resolved the vector into mutually perpendicular component. We can assign a value to these components (see figure 6).  Ly Lx        Figure 5   Figure 6   Figure 7   Figure 8 See figure 7.It shows two vectors linked head-to-tail, ready to be added. Let us 1)Resolve the vectors into orthogonal (it means "at right angles") components. (see figure 7). 2) Add the x-components together; add the y-components together. 3) add these two vector sums using the Pythagorean theorem to get the net sum (black dashed line). See the applet at http://canu.ucalgary.ca/map/content/vectors/basic/glimpse/ See the applet at http://canu.ucalgary.ca/map/content/vectors/basic/simulate/1/ VECTOR SUBTRACTION Just as vectors have the property to add, so too do they subtract. And like real numbers in algebra, the subtraction is not commutative. the order of operation does make a difference. See figure 9 below. To subtract two vectors, 1) (without changing their length or direction), place the two vectors tail-to-tail. 2) the difference (red minus black) is the (green) vector drawn from the head of the second vector to the head of the first. Figure 8 below shows Red minus black. We would have come to the same conclusion if we had ADDED red and the negative of black (see figure 11).             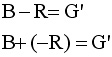Figure 9  Figure 10 Figure 11   Figure 12  Figure 13 Figure 14      Check this web site for a comprehensive view of this topic http://hyperphysics.phy-astr.gsu.edu/hbase/vect.html  The rules regarding vector addition prescribe that:   1) the length of arrows representing vectors should be proportional to the relative size of the vector quantities at hand;   2) we can move vectors anywhere in space provided we do not change their length or direction;  3) the addition of vectors is commutative (the sum is the same regardless of the order of addition). The problem set that follows will give you practice at dealing with this topic. http://www.msu.edu/user/brechtjo/physics/vectorAdd/vectorAdd.html http://www.pa.uky.edu/~phy211/VecArith/index.html    A good applet here http://www.explorescience.com/activities/Activity_page.cfm?ActivityID=23 collision in 2 D  361   Return to kinematics this page was reviewed 01/23/09.