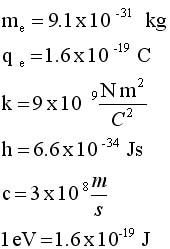The Bohr Model for Hydrogen
By 1913,
the state of physics was in some disarray with regard to atomic
structure. Rutherford had shone that a nuclear atom existed. But
that discovery led to two new questions, namely, 1) what holds
the nucleus together?; and 2) What mechanism of atomic structure
determines atomic volume? (We will hold off on a discussion of
Question 1 to another time.
The
query "What mechanism of atomic structure determines atomic
volume?" led to other difficult questions. a) If the negatively
charged electron is stationary, should it not be attracted to
a positive nucleus by Coulomb's Law? So what is the mechanism
that keeps them apart? b) If the negatively charged electron were
moving, it could be held in place by the Coulomb attractive force
of a positive nucleus. But James Clark Maxwell had shown decades
before that accelerated charges radiate energy. An electron orbiting
a nucleus is undergoing a centripetal acceeration and therefore
should radiate energy. But no such energy was found! Thank you
Mr. Rutherford!!!!
Enter
Neils Bohr, Danish physicist, age 26, stage left. He took the
bold approach to suggest that the angular momentum of the electron
orbiting the nucleus was quantised (that is, it can only take
on certain values) and that this quantisation took precedence
over the Maxwell assertion of accelerating charges radiating energy.
Please follow the algebra as it unwraps below. As a student you
need to know that the Bohr model was subsequently suplanted by
a quantun mechanical approach; the Bohr model is but a first order
approximation. That's too bad because you will never see a neater
solution to a complex problem as what follows
From classical
physics
The electrostatic force acts
as a centripetal force |
From quantum mechanics
the angular momentum of the
electron is quantized |
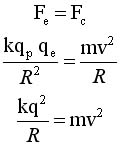 |
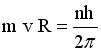 |
Solve for v and R
|
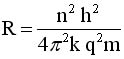 |
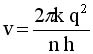 .. .. |
|
Evaluate these equations for v and r at n=1to n
= 5 |
Soooooo, because the angular momentum
is quantized, it turns out that
the space around the nucleus is quantized and so is the speed
of the electron.
|
Electron Energy Levels |
|
Substitute
for v & R
from above.
Watch the two
terms come
together.
This means that the
electron energy, shown
in line 5 at right,
is quantized
Prove that the
lowest energy
(ground state)
occurs when
n = 1 |
 EQ#1 EQ#1 |
|
Let's call this equation #1 |
Evaluate the energy for n = 2 & n = 3.
What is the difference in energies?
What wavelength is tied to this energy? |
|
E-level |
Energy
(in eV) |
level
transition |
change in
energy
(in eV) |
corresponding
wavelength
(in nm) |
color of
emitted
light |
|
6 |
-.37 |
from 6 to 2 |
3.03 |
410.1 |
violet 2 |
|
5 |
-.54 |
from 5 to 2 |
2.86 |
434.0 |
violet 1 |
|
4 |
-.85 |
from 4 to 2 |
2.55 |
486.1 |
blue-green |
|
3 |
-1.51 |
from 3 to 2 |
1.9 |
656.2 |
Red |
|
2 |
-3.40 |
x |
x |
x |
x |
|
1 |
-13.6 |
x |
x |
x |
x |
Remember that these energy
levels exist only if Bohr's speculation about angular momentum
is valid. A hint of validity was supplied some twenty - eight
years earlier, in 1885, by Johannes Balmer, a German high school
physics teacher and sometimes numerologistt (someone who studies
for numbers sake). Of course, no one knew at the time thatr Balmer's
discovery would have such import.
Balmer was curious about the wavelength of the four lines lines
of the hydrogen spectrum. His query "Are these four numbers
random or are they connected in some way?"His answer suggested
a connection among the numbers, although Balmer had no idea what
it meant. With the equation immediately below he could generate
the wavelengths for hydrogen as long as n was an integer greater
than 2. Why was it 2 and not another integer , say 3, 4, or 5
, he had no clue. But putting in place of 2 the integers 1, 3,
4, 5, produced other wavelengths in the infrared or ultraviolet
that had never been seen before. And when spectroscopists went
loking for these new lines they found them exactly where Balmer
had predicted.It is one thing to find a relationship among a few
numbers; it is something much more important when the new equationcan
predict things that are unknown.
The Balmer Equation
|
J. Balmer found that
this formula could
generate wavelengths

|
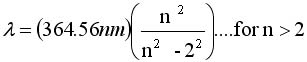 Let n = 3, 4, 5, 6 and
calculate the wavelength
Let n = 3, 4, 5, 6 and
calculate the wavelength |
Show that if we Rearrange terms and
Multiply by hc we can get Equation #2
|
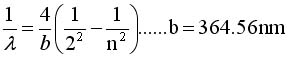 |
Calculate the
energy
|
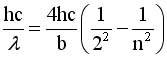 EQ
#2 EQ
#2 |
 EQ #1 EQ #1 |
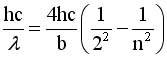 EQ #2
EQ #2 |
|
1. If we can show that these two
equations are equal, tthen we can use spectroscopy to analyze
atoms. |
|
|
2. Let delta E = hc/lambda for red light. |
|
|
3.The brachet in eq 1 = bracket in
eq 2 if n = 3 |
|
4. This works if  .
try it by plugging in the numbers .
try it by plugging in the numbers |
|
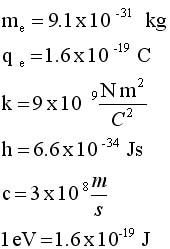 |
There are two ideas presented on
this page. 1) The space around the atomic nucleus is quantized;
electrons move from level to level by addition or removal of
definite quantities of energy.2) Spectral lines are tied closely
to these energy transitions. Studying atomic spectra gives us
a window to atomic structure. |
This interesting applet shows how electrons populate energy levels.
http://www.lon-capa.org/~mmp/period/electron.htm
Last edited 12/26/05
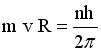
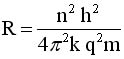
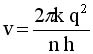 ..
..
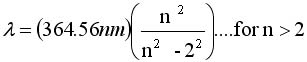
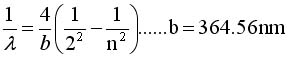
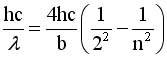 EQ
#2
EQ
#2 EQ #1
EQ #1