Interference in a one-dimensional medium

Consider a slinky stretched between two points. If we abruptly displace the spring at right angles to its length, a pulse is launched along the spring. If several pulses are created in short order, each will hold its place in line because waves travel at some characteristic speed for the medium. For pulses traveling in the same direction, watching this gets old early. But what if the pulses are headed toward each other on a collision course. What happens when they meet?
if the two combining pulses have displacements in the same direction, the displacements add constructively, momentarily producing a larger pulse, before continuing on as though nothing had happened. Think of this event as one wave climbing over the other. If the combining pulses have displacements on different sides of the slinky, the pulses combine to produce a smaller wave, perhaps even no wave at all. Once again the waves emerge from this momentary union as though nothing special had happened. Keep in mind that even if the two pulses disapppear for a moment, they must reappear. Each pulse carries energy;for them to combine destructively and vanish would be a violation of the law of conservation of energy. Visit the applets in the boxes below to get a feel for this

O-123

The simplest case: two pulses combining on a one-dimensional medium. http://www.phy.ntnu.edu.tw/java/wave/impulse.html http://id.mind.net/~zona/mstm/physics/waves/interference/waveInterference1/WaveInterference1.html http://www.phy.ntnu.edu.tw/java/waveSuperposition/waveSuperposition.html

Sine waves are easy to generate and relatively easy to add, although the sums can look pretty ugly pretty quickly. Try these on for size

O-124

Let's generate two transverse wave trains and add them together http://www.physics.brocku.ca/faculty/sternin/teaching/mirrors/superwaves/supers.html http://coral.lili.uni-bielefeld.de/~frederek/java/Sinus/added.html http://www.uno.edu/~jsulliva/java/superposition.html http://coral.lili.uni-bielefeld.de/~frederek/java/Sinus/added.html

Pretend that we send a series of pulses down a slinky that is tethered at the far end. The wave will reflect from the far end and return to the source with its displacement changed from a crest to a t rough and from trough to a crest. If the returning waves encounter new incoming waves that are identical, a wave pattern is created in which the waves simply undulate, that is, the left-to-right and right-to-left motion of the waves appears to vanish. Understand that a wave is moving through this space left to right and another right to left. The waveform only has the appearance of standing still and is called, sit down for this. a standing wave. This phenomenon has significant importance in music where standing wave patterns are the essence of resonance.
Resonance occurs when waves, previously created and sent through a medium, combine constructively wth new waves now being launched. Resonance is most easily explained using mechanical waves. Consider a child swingng on a swing at some frequency. Consider the parent as a pushing machine, extending his/her arms with the same frequency as the child. If the parent is properly placed, pushing forward just as the child arrives, the parent push adds to the child's displacement. If the parent is not properly placed, the parent push works against the swinging child's and resonance is not achieved.

O-125

http://icg.harvard.edu/~scia49/java/StandingWave.html http://www.phy.ntnu.edu.tw/java/waveSuperposition/waveSuperposition.html http://webphysics.davidson.edu/Applets/Superposition/Superposition_EX.html

For a good explanation of light interference, go to

http://www.colorado.edu/physics/2000/index.pl

Interference in a two-dimensional medium

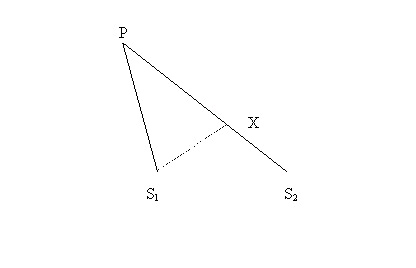	Consider two point sources ( S1 & S2) of waves producing transverse waves of some arbitrary wavelength on pan of water. For now the sources are in phase and produce identical waves at the same time. The waves emanate from each source as circular wave fronts traveling in all directions in this two-dimensional medium. We choose some arbitrary point P where we can observe how the contribution from each source will add together. The distance from a source to a point is called path length and could be measured in some conventional distance unit but is usually paced off in wavelengths of the wave being used. What happens at P depends on the difference in path length (PLD) from the two sources to P. In the diagram at left, S 1 P = XP. This leaves S2X = PLD. if the PLD is some odd multiple of half wavelength, we get destructive interference. If the PLD is some even multiple of half wavelength, we get constructive interference.
Visit Mr. Hwang's applet
Visit Mr. Hwang's applet and see a diagram similar to the one at left. Place the cursor where two crests meet; this is where one line crosses another (crest meets crest). Look at the path length difference illustrated in the box. You will note it to be very close to a whole number of (or even number of half) wavelengths. Now place the cursor at a point a where a line crosses a trough (the space between lines); this is a point of destructive interference. You will note that the path length difference is an odd number of half wavelengths.

These applets show in marvelous animation. the combination of waves produced b two point sources in phase. Think of the concentric dark circles as crests; the clear circles in between are troughs. The black "fingers" that show are zones of destructive interference.

These are called Moire patterns

http://www.msu.edu/user/brechtjo/physics/interference/interference.html
http://webphysics.davidson.edu/Applets/Ripple/Ripple.html
http://www.netzmedien.de/software/download/java/interferenz

http://surendranath.tripod.com/DblSlt/DblSltApp.html

http://www.phy.ntnu.edu.tw/java/doubleSlit/doubleSlit.html

http://www.microscopy.fsu.edu/primer/java/doubleslit/index.html

http://www.bpreid.com/samples.html

applet central
http://www.uncwil.edu/people/hermanr/phy101/Applets.htm

http://www.cbu.edu/~jvarrian/applets/waves1/lontra_g.htm

An applet view of the EM spectrum

http://www.colorado.edu/physics/2000/index.pl

Young's Two-Slit Experiment with Laser Light
http://www.colorado.edu/physics/2000/applets/twoslitsa.html

Constructive and Destructive Wave Interference
http://www.colorado.edu/physics/2000/applets/fourier.html

http://lectureonline.cl.msu.edu/~mmp/applist/Spectrum/s.htm

A double slit will separate white light into a continuous spectrum of visible color. What happens when a source gives off only a small portion of that spectrum?

Click on the element and see its bright line spectrum
http://javalab.uoregon.edu/dcaley/elements/Elements.html

http://www.phys.virginia.edu/classes/252/spectra.html

Go to http://www.glenbrook.k12.il.us/gbssci/phys/Class/light/u12l1b.html to view a site that closely models my classroom talk about this.

This first applet shows very nicely what happens to te light pattern when variables are changed
http://webphysics.ph.msstate.edu/jc/library/24-3b/simulation.html

http://www.holostudios.com/holohelper/interference.html

derivation of Young's experiment equations
http://www.phys.ualberta.ca/~trpk/phys100/physopt/lite_int.html


color sim
http://webphysics.ph.msstate.edu/jc/library/24-3b/simulation.html

http://www.phy.ntnu.edu.tw/java/propagation/propagation.html

This first applet shows very nicely what happens to te light pattern when variables are changed
http://webphysics.ph.msstate.edu/jc/library/24-3b/simulation.html
http://www.ece.gatech.edu/research/ccss/education/Java/1998.Winter/Projects/pierce-woods/project/bin/projApp.htm

This page was last modified by mgosselin on 10/08/2005