 |
|
|
 |
|
|
Newton's Law of Universal Gravitation
During
the plague years 1665-1666, Newton came to understand the mechanism
that tied the universe together according to a rule. It would
appear that he approached the problem from opposite venues. He
had been studying the path of the moon. What is now known as Newton's
first law suggests that if an object is moving with uniform speed
in a straight line, then Fnet
must be zero. That implies that if the
path of an object is not a straight line, then Fnet is not zero. From
that conclusion, we infer from the second law that, because Fnet is not zero,
the object must be accelerating -- even if it is moving at a constant
speed! Further, the acceleration must point in the same direction
as Fnet. From this Newton concluded that there must be something
at the center of the moon's path that supplied Fnet; but the only
thing there was the Earth.
Now comes the apocryphal story of Newton
sitting in his garden when an apple falls from tree. He ruminated
on how far up the tree and into the sky did this force go. He
speculated that the force might even extend to the moon and set
about calculating the acceleration that the moon should experience,
and compared that number to his estimate of what the Earth's acceleration
due to gravity would be at that distance and "...found that
they answered pretty nearly." Newton did the proof
geometrically using wretched British units. We can do it algebraically
with metric units and arrive at a conclusion similar to Newton's.
| Part 1. At the surface of the Earth (one Earth radius from the center of the planet), the acceleration due to gravity is g = 9.8 m/s2. At the site of the moon, some 240,000 miles (60 Earth radii ) away, Newton speculated that g = (1/60)2 times 9.8 m/s2. We calculate this quantity g = .00272 m/s^2 |
|
|
See this applet
This conclusion, that the force that
pulls things to Earth is the same force that keeps the moon in
its orbit , is called the
Newtonian Synthesis. No longer are there
separate rules for heaven and Earth.
Newton the introvert does not publish these thoughts because
he has no real need to show off. The information comes to light
when, at the behest of Edmund Halley, Newton published the Principia,
the first physics book.
The law of universal gravitation looks like this F = G M1 M2/d2
There is a problem with the units in this equation. The left side in modern terms would be measured in Newtons. The right side was more difficult because it is measured in kg2/ m2. Henry Cavendish was able to show using a very sensitive torsion balance that 1 kg2/m2 = 6.67x 10-11 N. Dividing both sides by kg2 and multiplying both sides by m2, we get 6.67 x 10-11 N m2/kg2 = 1. We shall rename the quantity on the left G - the Universal Gravitational Constant.
A carbonated beverage recently opened on the Earth undergoes a separation of matter that is caused by gravity (bubbles rise but water does not). What happens to the liquid and the gas if the mixture is aboard a space shuttle orbiting the Earth.
| http://www.phy.syr.edu/research/education/java/SUorbitnew/SUorbitnew.html | |
| http://www.mcasco.com/p1grav.html | |
| http://library.advanced.org/16600/intermediate/gravitation.shtml |
Satellite Motion
Planets around the sun
Combining the principle of universal gravitation with the concept
of objects moving in circular paths leads us to some remarkable
conclusions about the planets and about the technical hurdles
that must be overcome to put satellites in orbit around the Earth.
Consider a planet moving about the Sun in a circular orbit.
(Note that for the smaller planets close to the Sun, this is a
very good approximation.) Go to Equations,
either at this site or in the classroom. Find page 4, lines 4
& 5 and set the parts of the equations equal to each other
.
| If planets move in (nearly) circular orbits, some force must be acting as a centripetal force. The only candidate available is gravity. |
|
| See the Equations page, specifically page 4 |
|
| Let us tidy up the mathematics |
|
| The speed of an object can be determined by dividing the circumference of an orbit by the time it takes to travel that distance |
|
| Substitute line 4 into line 3 |
|
|
Solve line 5 for the mass of the sun. Note that the |
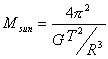 |
From these few lines of algebra we learn
1. We can calculate the mass of the sun
by observing a planet that orbits the sun.
2. By simple extension, we can calculate the mass of any planet
observing a moon that orbits the planet.
3. The term ![]() is precisely Kepler's
law of periods first set down in 1618.
is precisely Kepler's
law of periods first set down in 1618.
Satellites around the Earth
We can adapt the reasoning presented above to consider a human-crafted satellite (as opposed to the moon) in orbit about the Earth. it can be shown from the reasoning above (can you do it?) that the orbital velocity for this satellite is
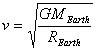
Go to References to find the pertinent
data then calculate the following
1. The orbital velocity (in m/s and mi/hr) of a satellite in
orbit at the surface of the Earth.
2. Determine the period (time for one orbit) for this satellite.
in the orbital velocity of a satellite around the Earth is about five miles a second something like17,600 miles per hour. Scientists have known about that number since 1799 wherein Henry Cavendish determined the universal gravitational constant. How absolutely absurd it must have been to consider something traveling five miles a second when the fastest being on the planet was a racehorse. for the next 150 years, travel beyond the confines of the earth was little more than dream.
Velocities approaching those necessary for orbiting this planet became attainable after World War II when the Soviet Union and Western powers assimilated German rocket scientists into their military programs to begin to exploit advances made by the Germans in the V-2 rocket program. During the 1950s United States and the Soviet Union began a serious attempt at launching satellites to orbit the Earth. This competition between the two countries to reach a space first was called a space race and the early milestones were won by the Soviet Union. In October 1957, the Russians launched Sputnik I, a small-payload satellite which took its temperature and transmitted data to ground stations. The first craft launched by the United States to attain orbit was Vanguard 1 launched from Cape Canaveral in Florida in January 1958. In between 1958 and in 1961 the Russians launched the first dog in space, the first man in space, first woman in space John Glenn orbited the Earth three times in February 1961.
These early launches had scientific as well as political value on a planet caught up in a cold war. The first commercial application of satellite technology came in 1963 when the United States launched Telstar I, the first communications satellite. Telstar was placed in near-Earth orbit to serve as a relay link between NorthAmereica and Europe. The U.S. ground station was located in Andover Maine, near Bethel. But because Telstar was in near-Earth orbit, it was in proper send/receive position for only about 15 minutes every 90-minute orbit, a good first try but unacceptable by modern standards.
Syncom I launched in 1964 was placed in geosynchronous orbit above the equator. When properly placed, these satellites maintain a fixed position above some point on the equator and thus are always in position to send and receive transmissions. Let us calculate the speed and position of such a satellite.
|
This is the equation for the orbital
velocity of a satellite, as derived above. |
|
| The speed of an object can be determined by dividing the circumference of an orbit by the time it takes to travel that distance. In this case let T = 24 hours |
|
| Set cell 1 = cell 2 |
|
| Square both sides |
|
| Solve for R |
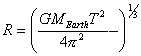 |
| R calculates to be about 26,000 from Earth center, or about 22,000 miles above the surface.Any other placement is said to be a useless orbit for a communication satellite. | |
Here is an applet where you can adjust the launch velocity for a projectile causing it to travel further and further down range until it has become an Earth satellite. http://www.phys.virginia.edu/classes/109N/more_stuff/Applets/newt/newtmtn.html
a) How large must the launch velocity
be to cause the satellite wanna-be to strike Earth at points A
or B?
b) What must be the minimum velocity of projection to cause
the satellite to orbit the Earth?
| http://ericir.syr.edu/Projects/Newton/12/Lessons/gravity.html | |
| http://ericir.syr.edu/Projects/Newton/11/blckhole.html |
On-line - stacking blocks
http://www.phy.ntnu.edu.tw/java/block/block.html
see also
|
|
Go to supplementary problems - gravity
Go to problems at U Oregon
http://www.zebu.uoregon.edu/~probs/mech/grav.html
Acceleration due to Gravity
From an extension of Newton's second
law, we know that the weight of an object is given by w = mg,
where w = weight, mo = mass of the object in question, and g is the
resulting acceleration is the object is allowed to move freely
between points. But weight is also the force of attraction between
the Earth and the object. Therefore,
mog
= G mo M Earth/(REarth)^2 . Canceling the mass of the object, we get
g = G M Earth/(REarth)^2 . That means the the local value of g depends
on the mass of the Earth, which is very nearly unchanging, and
the distance for the center of the Earth to where you are standing.
Had the Earth been slightly more massive or very slightly smaller,
the value of g would have been a more convenient 10 m/s/s.
This page last edited 01/24/09