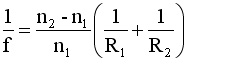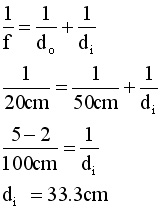we have seen in the previous section on refraction that when light rays strike that boundary between two transparent media at some oblique (read: non-zero) angle, the path of the rays changes in a predictable way known as Snell's Law. Visualize now several rays parallel to each other and incident on a rectangular glass slab situated in air. The angle of refraction is the same for each ray in glass so that the rays are still parallel to each other, even if they are now moving in a new direction. The rays now cross the slab of glass and are incident on the opposite face, striking it at the same angle (actually, can you prove this?) as was the angle of refraction in glass at the other surface. The rays now emerge into air all at the same angle, actually equal to the original incidernt angle; (psst? can you prove this?.) The only thing the glass has done has been to shift the bundle of rays to one side of the original path before the refraction took place. Not very exciting. But what would be the result if the air-glass boundary were cut into some useful shape? Try this.
ACTIVITY 1
1. Draw a diagram thar represents a rectangular glass block in air.
2 Draw at least three rays that are incident on the air-glass boundary. It may prove useful to cause these rays to be incident normally on the block.
3. Now carefully shape the first surface of the slab so that it is convex.
4. The normal lines are not parallel to each other any more (This is a critical fact.) Draw in the normal lines at the points of incidence on the surface.
5. Cause the lines crossing the air-glass boundary to refract. Notice that the rays of light are made to come together (does the word converge come to mind?)
6. Now cut a second convex surface on the far side of the glass slab. Repeat steps 4 & 5 above. What do the rays do now as they exit the glass?
7. There is insight to be gained by the student who repeats this activity with a double concave lens, a convex meniscus and a concave meniscus.It would be useful to know where these rays came to focus and precisely how index of refraction and shape of refracting surfaces together deteremined light paths. The equation in question is the lens-makers' equation given by
Where
n2 = index of lens material
n1 - index of material surrounding lens
R1 & R2 are radii of each lens surfaceIf f >0, lens is converging; if f < 0, lens is diverging.
ACTIVITY 2
Show that double convex and convex meniscus lenses are converging lenses.
Show that double concave and concave meniscus lenses are diverging lenses.ACTIVITY 3 - Simple lens lab
http://www.phys.ufl.edu/~deserio/simplens/simplens.htm
Clearly, refraction is more complex than reflection, because the path of a ray depends on the curvature of the refracting surfaces as well as the index of refraction of each material at the interface. It can be shown that the lensmaker's formula yields another useful relationship for lenses; this one is called the thin lens formula and is shown in the box.
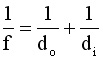 |
|
do = distance from object to lens di = distance from image to lens |
| The relative size of image to object is called magification |
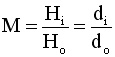 |
|
A lens is thin when its maximum thickness is relatively small when compared to object and image distances. When this condition is in place, the equation is very useful for locating images. Let's look at it in more detail.
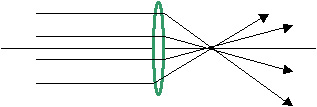
|
Case
1. Object at infinite distace from lens. Let us examine the thin lens formula carefully. Because the shape of the lens does not change, the left-hand side is fixed and unchanging. If we alter do, making it larger and larger, di has to get smaller and smaller. Makinig do as large as possible reduces the fraction 1/do to zero and making di = f. The distance f. called the focal length, represents the point of closest approach of the real image to the lens. This point is called the focal point of the lens. Every lens has two focal points, equidistant on either side of the lens. In the diagram at left, rays have traveled so far from infinity that they reached the lens parallel to each other. These rays strike the lens and then they pass through the focal point. |
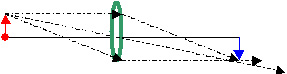 |
Case 2. 2f < do
< infinity If one moves the object closer to the lens, the image moves away from it. SEE THE APPLET BELOW. As long as the object distance is greater than twice the focal length of the lens, the image will be a distance less than twice the focal length of the lens. Careful examination of the magnification equation will show that the magnification of this image is less than one, making the image smaller than the object. |
 |
Case 3. do = 2f For any given focal length, it turns out that if object distance equals twice the focal length of the lens, the image distance will also equal twice the focal length. SEE THE APPLET Magnification will be equal to one size of the image equals the size of the object |
 |
Case 4. f < do
< 2f When the object is a distance from te lens greater than the focal length but less than twice the focal length the image falls beyond the second focal point and is a distance away from the lens much greater than two times the focal length |
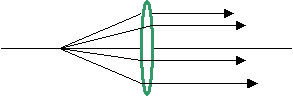 |
Case 5. do = f Placing the object at the focal point will cause the object distance equal to the focal length. A necessary consequence of this action is to show the image forming at infinity. All rays leaving the focal point will strike the lens and emerge from the lens parallel to each other. Therefore they do not converge; in mathematics owe say the converge at infinity |
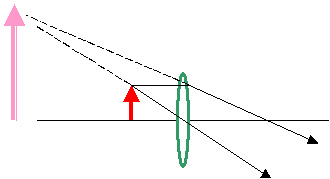 |
Case 6 zero < do <
f In this case, light rays emerging from the lens are diverging. That means they will never form a real image. when these diverging rays enter the eye, they appear to come from a virtual image on the same sign of the lens is the object. This image is usually much larger then the object that created it SEE THE APPLET |