|
|
|
|
|
We see objects because one of two phenomena is at work. Either a) the object is luminescent and gives off its own light; or b) the object reflects light from other sources. Most objects fall into category b) and reflect light irregularly because they have rough and uneven surfaces. This is called diffuse reflection. But when the surface is smooth and formed into some regular shape, the direction that reflected light takes becomes very predictable.
 |
|
|
|
Check these web sites to learn
more about the Laws of Reflection.
| O-01 | http://id.mind.net/~zona/mstm/physics/light/rayOptics/reflection/reflection1.html |
| 361 | Visit HYPERPHYSICS and check out this topic. |
| 368 |
The
usual fine treatment from Glenbrook http://www.glenbrook.k12.il.us/gbssci/phys/Class/refln/u13l3a.html |
|
Interesting sidebars from the Exploratorium http://www.exploratorium.edu/snacks/iconreflection.html Good stuff from ASU http://acept.la.asu.edu/PiN/rdg/reflection/reflection.shtml |
| O-02 | http://www.phy.ntnu.edu.tw/java/optics/mirror_e.html |
|
mirror game http://www.phy.ntnu.edu.tw/java/optics/mirrorgame_e.html |
|
|
multiple reflections with two mirrors http://www.phy.ntnu.edu.tw/java/index.html /applets/planmir/Welcome.html |
|
| http://micro.magnet.fsu.edu/primer/java/scienceopticsu/hinged/index.html | |
|
Plane mirror applet by Prof. Hershfeld http://www.phys.ufl.edu/~phy3054/light/mirror |
|
Image Formation
Mirrors (and lenses as we shall see later) can form two different kinds of images - virtual images and real images. Their collected properties are listed in the table here.
|
|
|
| Formed by mental extension of rays | Formed by converging rays |
| Cannot be projected on a screen | Can be projected on a screen |
| Not inverted | Inverted |
| Perverted | Not perverted |
When light leaves an object, the rays travel by diverging from the object. Placing a plane mirror near some object will redirect the rays to a new path; nevertheless, the rays continue to diverge. If these rays are intercepted by your eye, your brain recognizes this pattern of diverging rays and mentally extends them straight back to some point on the other side of the mirror glass. Hence the image appears to be behind the mirror. This kind of image is called a virtual image (no, there is no connection to virtual reality) and possesses the properties shown in the box above. These properties come in an unbreakable set; if one property is true, they are all true.
| If a mirror reverses left and right, why does it not reverse top and bottom? Answer: It does not reverse top and bottom because it does not reverse left and right. The image you see in a plane mirror is 'perverted' by which I mean that it has been turned inside out, as a latex mask of your face could be removed and turned inside out. Because you face is not perfectly symmetrical, your perverted image and the real you as seen by everyone else are not identical. To witness this effect, look in a plane mirror at the virtual image of someone you know well (a parent or sibling will do). Do they look different? The truth is, that different look is what your parent/sibling always sees when he/she looks into a plane mirror. This matter of what you look like as seen by you in a mirror vis-a-vis what you look like to someone else is analogous to hearing your voice as you speak compared to hearing your voice tape-recorded. |
| One-way glass. A mirror is made by depositing a metal coating on a piece of plate glass. Deposit a full coating onto the glass and atoms in sufficient number reflect most of the light (while absorbing a small amount through inefficiency). Deposit less than 100% coating, some light gets through. The curious thing is that the passage of light from one side to the other happens either way with equal facility. In any surveillance situation,the room in which the watchers are standing should be dark. |
| Reflections from windows at night. Objects in a room form virtual images on window glass. Where are those images during daytime? Answer: during the day the reflected light,which is about 10% of the incident light, is overpowered by daylight coming from outside. |
| "Transporter" room. In the early years of Star trek, the actors would go to the transporter room, stand at their places, their images would be covered over with a little fuzziness and they were gone. . Here is what really happened. When the actors took their places in the transporter room, situated in front of them was a large sheet of plate glass positioned diagonally across the stage. On the other side of the glass from the actors is another transporter room. The lighting director simply lowered the lights on one side of the glass and raised them on the other |
| A kaleidoscope is a simple toy that creates interesting images through multiple reflections. Consider three mirrors each 3 cm wide and 20 cm long. Arrange the mirror pieces so that they touch along their long edges to form a triangular prism. The reflective surfaces should be on the inside. Look through one end of the prism |
| Rearview mirrors and bright high beams. Like any other mirror, a rearview mirror relies on its reflective coating for its reflective properties. When the car behind your vehicle shines high beams into your mirror, you can flip the mirror n such a way that the reflective coating is out of the picture. The reflecting now happens on the front of the glass where 10% of incident light is now a good thing |
| CAUTION objects are closer to the mirror than they appear For most people using a mirrors means using plane mirrors. If an observer is looking into a plane mirror, very distant objects would produce a very small images... On the right hand side of most cars is a convex mirror intended to show much of the space behind the right side of the car.Images produced by convex mirrors are virtual and are considerably smaller than the objects that produce them. the message tells the user that something special is manipulating the size of the image. |
| cube corner Picture if you will three mirrors that are mutually perpendicular, coming together in the corner of cube. It can be shown in any ray of light that strikes the first mirror will be reflected to the second mirror and then to the third and then exit that arrangement exactly parallel to the direction of the original incident beam. Such a device is vital whenever a ray needs to be reflected back to the point from whence it came |
| A kaleidoscope is a simple toy that creates interesting images through multiple reflections. Consider three mirrors each 3 cm wide and 20 cm long. Arrange the mirror pieces so that they touch along their long edges to form a triangular prism. The reflective surfaces should be on the inside. Look through one end of the prism |
CURVED MIRRORS
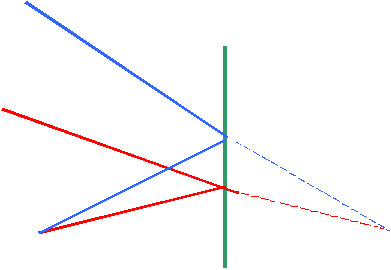
A curved mirror can yield results that are quite different from the images produced by a plane mirror. Most commonly in an introductory course such as this, we deal with concave spherical mirrors. Picture a basketball about a meter in diameter. We coat the inside of the sphere with a reflecting surface and then (mentally anyway - this is not an industrial process) we cut out a piece using a cookie cutter. This mirror produces a different kind of image than does a plane mirror. Rays of light leave some point on an object and diverge on their way to the mirror. Having struck the mirror, they converge to a point in space. From that point rays continue diverging to the observer's eye. This is an example of a real image. See the list of properties for real images.actually whether a real images produced or not depends upon distance from object to mirror. Under certain circumstances in concave spherical mirror can produce an enlarged virtual image
if you coat the outside of
the basketball, a
convex spherical mirror
is produced. this kind of a late if the mirror produces only
virtual images and a smaller than you can be created a they have
limited use The rules that govern where and what kind of image
will be formed for all three mirrors are summarized on the page
called mirror conventions.
Applets aweigh
If we place
an object in front of a concave mirror and sufficiently far from
the mirror, we find appearing in space in front of the mirror
(and not behind it like the virtual images) an image that is
inverted. We call this kind of image a real image,
the properties of which are listed in the box above. As before,
the rays leaving the object are diverging-they leave the object
never expecting to see each other again. But because the mirror
is curved the way it is, the rays come together at a point in
front of the mirror. the rays pass through this image point and
then diverge from there on their way to nowhere in particular.
if those now newly diverging rays are intercepted by someone's
eye, the eye and brain will conclude that there is something
at the image point. There is a mathematical relationship that
governs where the image will be located; it's called the Gaussian
mirror formula and looks like this
|
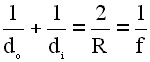 |
In this formula do is
the distance from object to mirror, di is the distance
from image to mirror and R is the radius
of curvature. Click here for the
derivation.The rules governing the algebraic signs for these
distances are given in the mirror conventions
page.
Go
to problem set 1 - plane mirrors
Go to problem set 3 - curved
mirrors